RMSProp／Momentum／Adam／AdamW，多种优化器详解及伪代码实现_1

更新时间：2024-05-13 09:44:55

标签： bert 调参 NLP

多种梯度更新方法——都是对Gradient Descent的优化

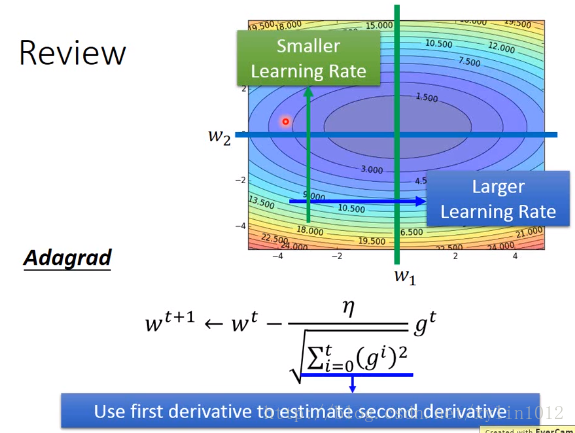
在这里插入图片描述

为了解决不同方向上梯度涨落速度不一致的情况，所以相当于给每个方向不同的learning_rate。

具体每个方向的lr大小要怎么拟定？——之前该方向上grad大的，就给小lr——即梯度变化幅度缓慢，那么就拉开步子大胆走。如上图的公式，历史grad总量和lr大小成反比，即该方向的总grad越小，则lr就越大。

但该方法解决不了，在该方向上梯度先大再小的情况（如 RMSProp 图一）。

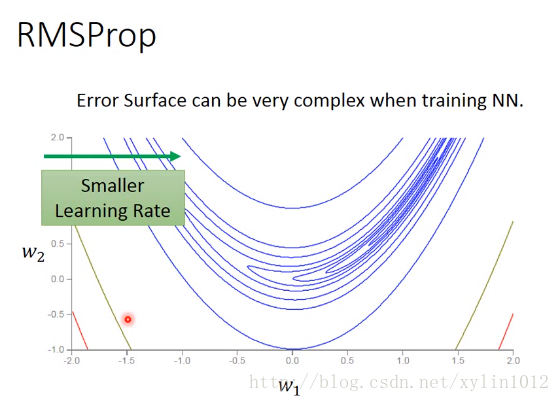
在这里插入图片描述

如图一， RMSProp 可解决这种grad在某一方向一会儿变化缓慢一会儿变化剧烈的情况
具体公式如图2.注意公式中的，可将之看作“decay_rate”，它相乘的，保存了全部的历史的grad，即。通过调整的大小，可权衡新的lr是偏向新grad还是历史grad。
实际上的RMSProp公式和这里的稍有出入，见下图3。RMSProp共有2个超参数，对下图而言，就是和，这里对应李宏毅教程就是，我们还是称之为。

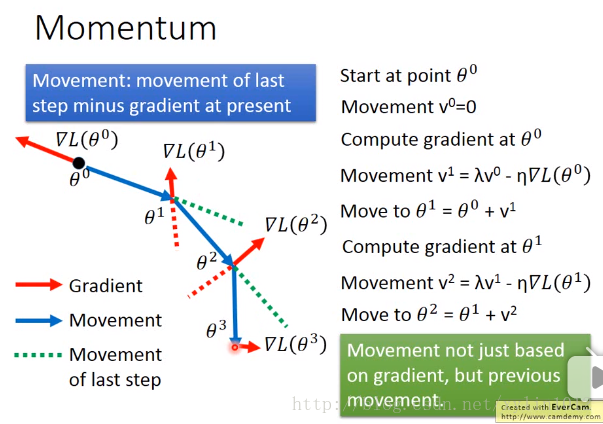
在这里插入图片描述

超参数： ,

在这里插入图片描述

思路：梯度的更新，应考虑到此前梯度的变化情况——这次是在方向上的考虑，即加上“惯性”。其中，原梯度越大，对下一步梯度的“转向影响程度”越大。
该方法有一个超参数，每一步真实的梯度，从原求导结果变为了。

需要注意的是，momentum和以上两个方法不太一样。以上两个还可以被称为对学习率的调整，但momentum和学习率无关，它的改动项直接加在学习率和原梯度的乘积上。

超参数：

在这里插入图片描述

如图所示，是Adam优化器的伪代码。我们详细来看

首先，看数字1标识处：对参数进行初始化。其中是Momentum，指的是动量，即使用历史梯度平滑过的梯度；是RMSProp式中的 (见李宏毅RMSProp部分的slide截图)，即记录了全部历史grad，并用此进行梯度的指数加权平均。
绿色五角星：循环条件——被优化的参数没有收敛。这个没啥可说的~
数字2标识处：首先，当然是通过当前batch计算这一步的梯度
数字3标识处：先计算即动量momentum，并涉及第一个超参数。其实这里算法和momentum是几乎一样的，所以这里的作用也是对历史梯度和当前梯度的衡量；
数字4标识处：RMSProp的因数计算，和RMSProp里计算步骤完全一样，略
5.1、5.2：bias-纠正计算，没仔细了解就不妄下结论了
数字6：将结果整合到一起，更新参数的梯度

简单来说，AdamW就是Adam优化器加上L2正则，来限制参数值不可太大，这一点属于机器学习入门知识了。以往的L2正则是直接加在损失函数上，比如这样子：
$Loss=Loss + \frac{1}{2}\lambda\sum_{ heta_i \in \Theta} heta_i ^2$
但AdamW稍有不同，如下图所示：
在这里插入图片描述
粉色部分，为传统L2正则施加的位置；而AdamW，则将正则加在了绿色位置。至于为何这么做？直接摘录BERT里面的原话看看——

总之就是说，如果直接将L2正则加到loss上去，由于Adam优化器的后序操作，该正则项将会与和产生奇怪的作用。具体怎么交互的就不求甚解了，求导计算一遍应该即可得知。
因而，AdamW选择将L2正则项加在了Adam的和等参数被计算完之后、在与学习率lr相乘之前，所以这也表明了weight_decay和L2正则虽目的一致、公式一致，但用法还是不同，二者有着明显的差别。以BERT中的AdamW代码为例，具体是怎么做的一望便知：

如code，注意BERT这里的就是当前的learning_rate。而最后两行就涉及的计算。如果我们将AdamW伪代码第12行的公式稍加化简，会发现实际上这一行大概是这样的：
$heta_t= heta_{t-1} - lr * grad_ heta - lr * \lambda* heta_{t-1}$
此处 $\lambda$ 就是。再将上述公式最后一项和code最后一行对比，是不是一模一样呢。

本文链接：https://blog.csdn.net/weixin_41712499/article/details/107231247

梯度下降优化算法的概述：SGD，Momentum，AdaGrad，RMSProp，Adam 最近有用到Adam优化器寻思了解下，找了些博客看看，大多是对比及几个的优劣，看不太懂，于是看了Sebastian Ruder的An overview of gradient descent optimization algorithms ，大佬就是大佬分析的非常透彻。特分享自译的版本。 1.Gradient...

原创不易，转载请注明出处文章目录 1 mini-batch 1.1 为什么用mini-batch？ 1.2 会什么代价还会变高(有波动) 2 指数加权平均 3 动量梯度下降法(Momentum) 4 均方根传播(RMSProp) 5 自适应估计(Adam) 6 pytorch调包 7 学习率衰减像梯度下降法这样的，通过偏导来优化参数，统称的优化算法优化算法：为了寻找最优参数，提升模型训练的速...

一、optimizer 算法介绍 1、Batch Gradient Descent(BGD) BGD采用整个训练集的数据来计算 cost function 来进行参数更新。 θ=θ−α⋅∇θJ(θ) heta= heta - \alpha \cdot abla_{ heta}J( heta...

先放一张公式汇总图： Contents 1 Momentum动量优化算法 1.1 梯度下降的问题 1.2 动量法 1.3 动量法的简洁实现 2 ADAGRA算法 2.1 算法简介 2.2 从零开始实现 2.3ADAGRAD简洁实现 3 RMSprop算法 3.1 算法简介 3.2 从零开始实现 3.3 RMSprop简洁实现 4 AdaDelta优化算法 4.1 算法简介 4.2 从零开始实现 4...

在网上看到有关各种分类器的讲解：优化器算法Optimizer详解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam）英文原文传送门中文翻译版传送门机器学习算法的目标机器学习和深度学习的目标是减少预测输出与实际输出之间的差异。这也称为成本函数（C）或损失函数。成本函数是凸函数。我们的目标是通过找到权重的最佳值来最小化成本函数...

系列文章目录人工智能—梯度下降的原理和手写实现文章目录系列文章目录前言一、梯度下降优化器是什么？二、SGD优化方法 1.SGD是什么 2.SGD的数学原理 3.SGD的实现 4.SGD的缺陷三、Momentum优化方法 1.Momentum是什么 2.Momentum的数学原理 3.Momentum的实现 4.Momentum的优势四、AdaGrad优化方法 1.Ada...

说明模型每次反向传导都会给各个可学习参数p计算出一个偏导数，用于更新对应的参数p。通常偏导数不会直接作用到对应的可学习参数p上，而是通过优化器做一下处理，得到一个新的值，处理过程用函数F表示（不同的优化器对应的F的内容不同），即，然后和学习率lr一起用于更新可学习参数p，即。 RMSProp原理假设损失函数是，即我们的目标是学习x和y的值，让Loss尽可能小。如下是绘制损失函数的代码以及绘制出...

1. Adam optimizer adam优化器是经常使用到的模型训练时的优化器，但是在bert的训练中不起作用，具体表现是，模型的f1上不来。 2. AdamW transformers 库实现了基于权重衰减的优化器，AdamW，这个优化器初始化时有6个参数，第一个是params，可以是torch的Parameter，也可以是一个grouped参数。betas是Adam的beta参数，b1和b...

13.4 再谈边缘检测在12.3中，我们曾使用Sobel算子对屏幕图像进行边缘测试，实现描边的效果。但是，这种直接利用颜色信息进行边缘检测的方法会产生很对我们不希望得到的边缘线，如图13.8所示。可以看出，物体的纹理、阴影等位置也被描上黑边，而这往往不是我们希望看到的。在本节中，我们将学习如何在深度和法线上进行边缘检测，这些图像不会受纹理和光照的影响，而仅仅保存了当前渲染物体的模型信息，通过这...

目录前提整体机制写隔离读隔离工作机制一阶段二阶段-回滚二阶段-提交附录回滚日志表前提基于支持本地 ACID 事务的关系型数据库。 Java 应用，通过 JDBC 访问数据库。整体机制两阶段提交协议的演变：一阶段：业务数据和回滚日志记录在同一个本地事务中提交，释放本地锁和连接资源。二阶段：提交异步化，非常快速地完成。回滚通过一阶段的回滚日志进行反向补偿。写隔离 ...

上一篇：15部门：全面加强经营性自建房安全管理

下一篇：抖音下载视频怎么取消水印？

[返回列表]